Methodology

This section provides technical details regarding the algorithm used to create octree meshes.

An octree mesh is a discretization of a 3D volume into a set of rectangular cells. The cells are defined by a tree structure, where each node has 8 children. The tree is grown by splitting each node into 8 children, until a minimum cell size is reached. The figure below shows an example of an octree mesh along a cross-section.

We define cells with the same size as a level of the tree, where the smallest cell size corresponds to Level 1.

The entire octree creation process can be broken down into two main steps:

• Creating the base mesh (General Parameters) that defines the outer extents, core cell and padding parameters.

• Refinining the grid (Optional Parameters) to increase the resolution of the mesh in specific regions based on a set of rules.

Creating the base

This step relies on the discretize.utils.mesh_builder_xyz method to create the base mesh (single large box). The following general parameters provide controls on the position and outer limits of the mesh.

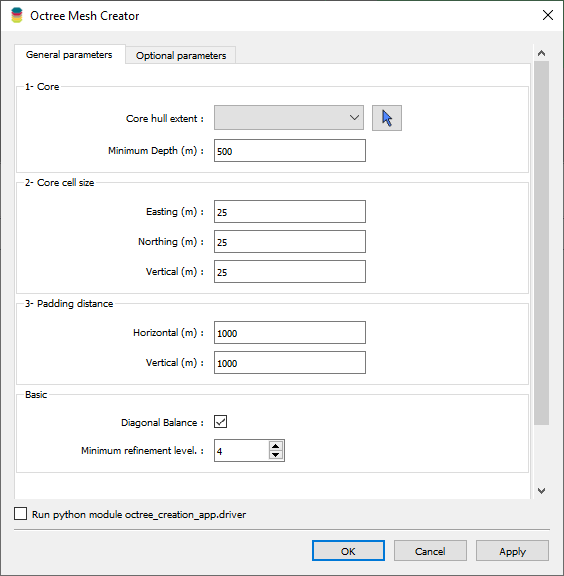
• Core hull extent:

  List of objects available in the target geoh5 project. The base mesh fully contains the hull of the selected object. If the mesh is to be used towards a forward simulation or an inversion, the object would be the survey entity.

• Minimum depth:

  Thickness of the mesh added below the core region. This is useful to ensure a minimum thickness of the mesh that extends below the lowest point of the input object.

• Core cell size:

  • Easting (m): Smallest cell size along X-axis, in meters.

  • Northing (m): Smallest cell size along Y-axis, in meters.

  • Vertical (m): Smallest cell size along Z-axis, in meters.

• Padding distance:

  • Horizontal (m): Distance to extend the mesh along the XY-plane.

  • Vertical (m): Distance to extend the mesh above and below the core + minimum depth.

  Note

  Setting the vertical padding = 0 will place the top of the mesh at the highest elevation of Core hull extent object. This is useful for creating a mesh that minimizes the amount of air cells.

• Diagonal Balance:

  If checked, the mesh is refined such that any pair of cells sharing a node can increase in size by at most one octree level. The figure below demonstrates the effect of this option on the refinement of a mesh.

  Balanced	Not balanced

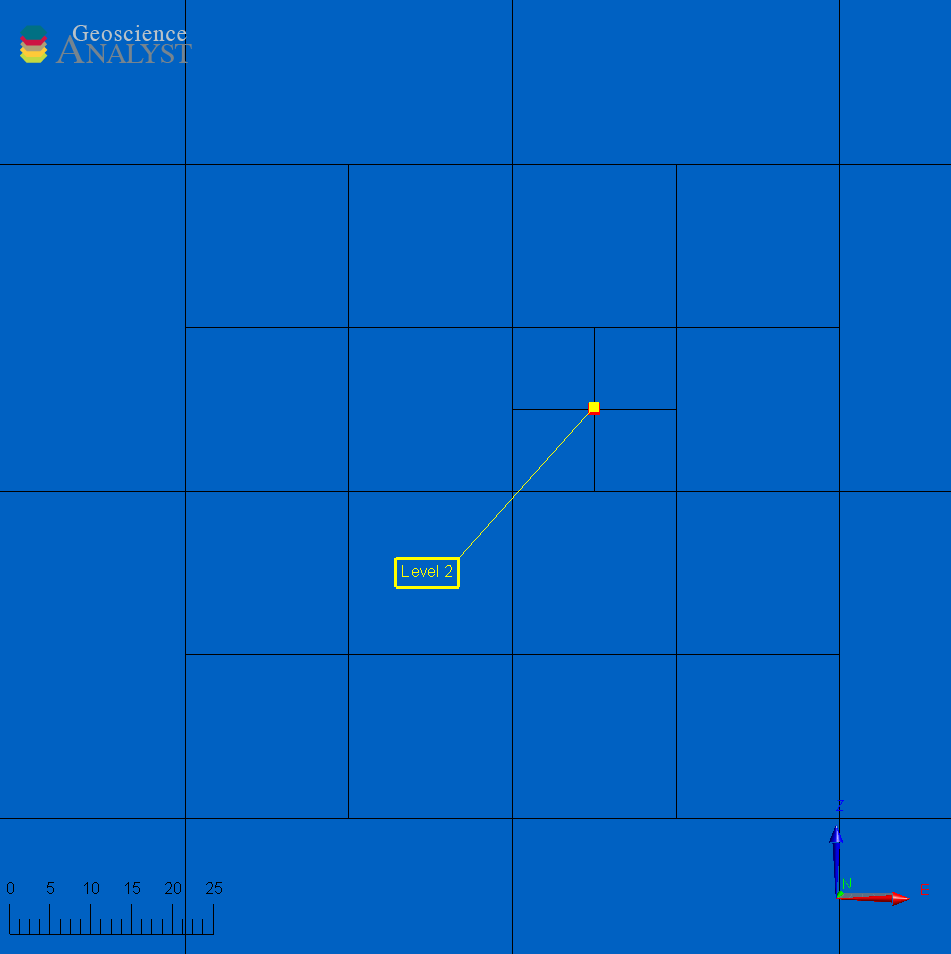
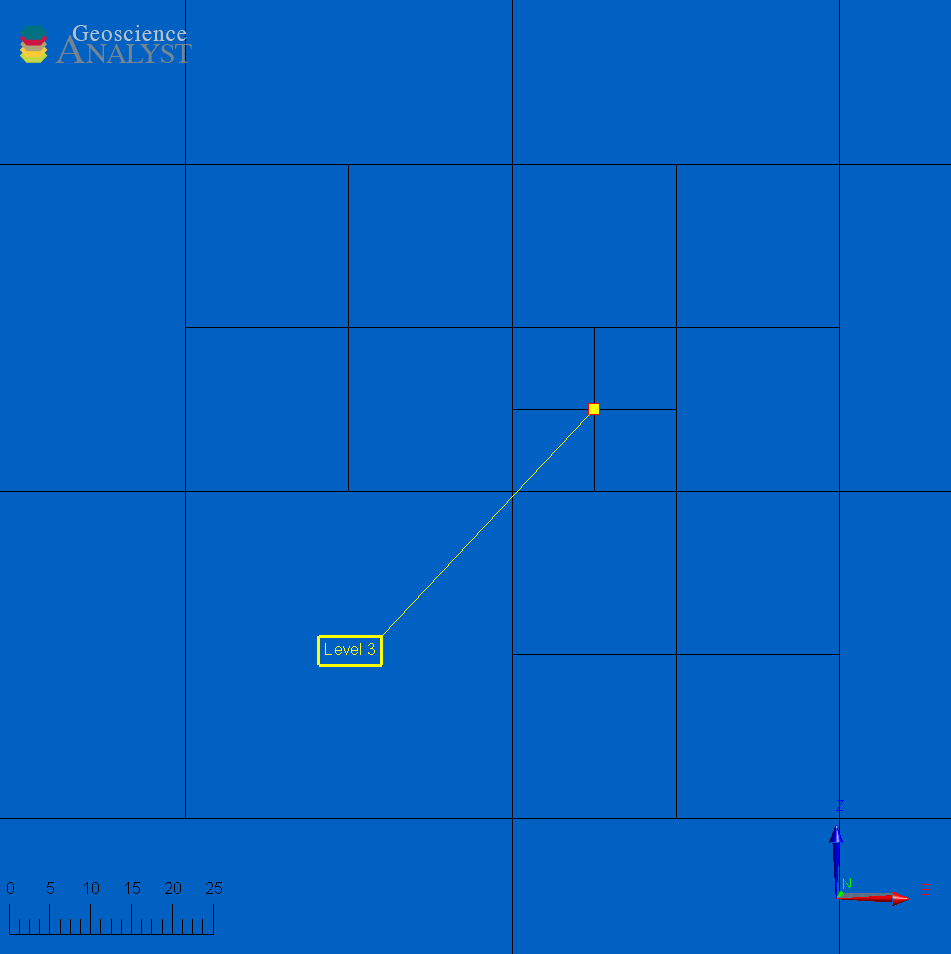
  Note that the mesh without diagonal balance is allowed to go from octree Level 1 to Level 3 across cells sharing a corner. This would result in overall fewer cells in the mesh but can decrease the accuracy of the forward simulation when solving partial-differential equations. The diagonal balancing is required for compatibility with UBC-GIF software.

• Minimum Refinement:

  Largest octree level allowed after refinement. The equivalent cell dimension is given by:

  \[h \times 2^{level - 1}\]

  where h is the core cell size in a given direction. This option is useful to ensure that the mesh does not become too large away from the core region.

Example

The example below demonstrates this process with simple line survey shown below and the following parameters:

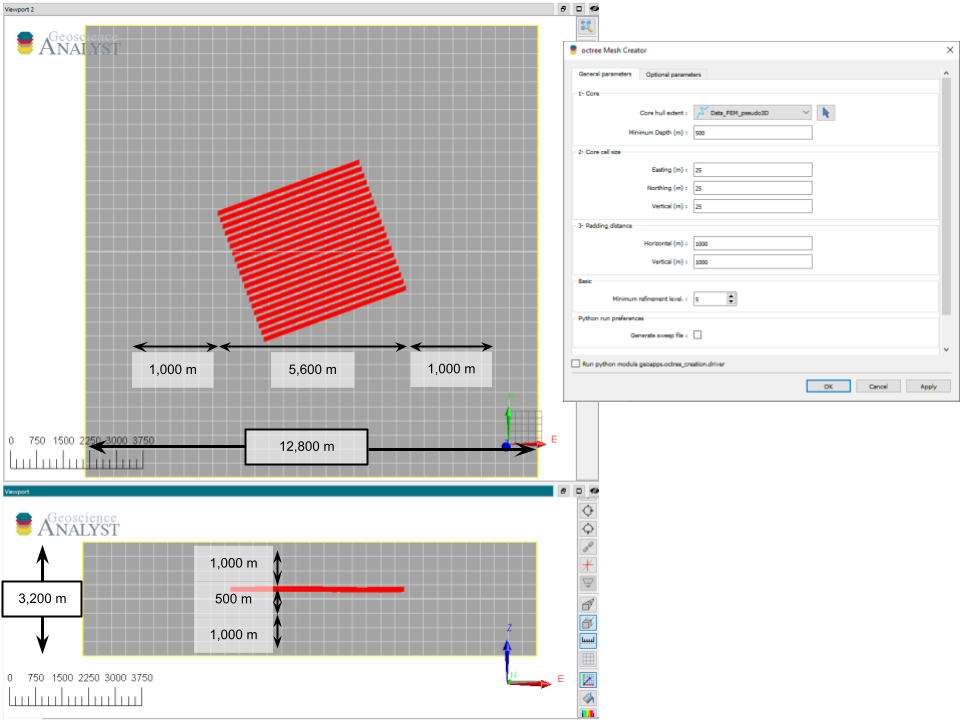
Fig. 1 Section through an octree mesh for parameters used in the example below. The input survey object is shown in red. Distances have been annotated to clarify the dimensions of the input parameters (right) and the resulting mesh (left).

(Top) Horizontal and (bottom) vertical E-W section through the same mesh.

Horizontal extent

• Input:

  • 5,600 m (survey hull)

  • 2 * 1,000 m (padding distance)

  Total: 7,600 m

• Number of cells:

  \[\begin{split}\frac{7,600 \;m}{25 \; m/cell} = 304 \; cells \\\end{split}\]

  Round up -> 512 cells

• Final dimensions:

  \[512\;cells \times 25 \frac{m}{cell} = 12,800\;m\]

Vertical extent

• Input dimensions:

  • 46 m (survey hull)

  • 2*1000 m (vertical padding)

  • 500 m (depth core)

  Total: 2,546 m

• Number of cells

  \[\begin{split}\frac{2546 \; m}{25\; \frac{m}{cell}} = 102\; cells \\\end{split}\]

  Round up -> 128 cells

• Final dimensions:

  \[128 \; cells \times 25 \frac{m}{cell} = 3,200\;m\]

Minimum refinement

• Input:

  • 25 m (core cell size)

  • 5 (minimum refinement)

Largest cell dimension:

\[25\;m \times 2^{(5-1)} = 400 m\]

The final mesh expected would be a 512 x 512 x 128 cells mesh, with an extent of 12,800 x 12,800 x 3,200 m. Note that the cell size is uniform and equal to the minimum level of 5 (400 m cell size), as defined in the parameters.

Refinements

Once the extent of the mesh has been defined, the user can increase the resolution (add small cells) in specific regions of the mesh based on a set of rules.

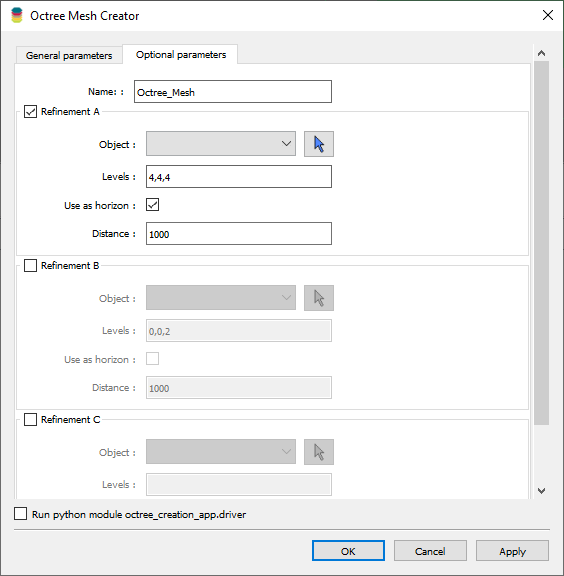
Up to three refinement strategies can be applied to the mesh. In regions where no refinement is provided, the cell size will double in size until reaching the minimum refinement level.

For every refinement strategy, the user must specify the following parameters:

• Object:

  Geoh5 entity to be used for refinement. The type of the object dictates the method of refinement.

  • Points -> Add concentric shells of cells around each vertices.

    Uses the refine_tree_from_points method.

  • Curve -> Add concentric cylinders of cells around each segment of the curve.

    Uses the refine_tree_from_curve method.

  • Surface -> Refine the mesh on the faces of a triangulated surface in 3D.

    Uses the refine_tree_from_triangulation method.

• Levels:

  List of integers defining the number of cells requested at each octree level.

  \[[1^{st}, 2^{nd}, 3^{rd}, ...]\]

• [Optional] Use as horizon:

  If checked, the object is used as an horizon with the refine_tree_from_surface method instead of the default method. The vertices of the object are converted to a Delaunay surface, which is then used to refine the mesh as layers of cells below the surface.

  • Maximum distance:

    Maximum distance from the object’s node to allow refinement. Cells are allowed to expand in size beyond this distance.

Refine by points

This method refines an octree mesh radially from the vertices of an object. It relies on the refine_tree_from_points method

static OctreeDriver.refine_tree_from_points(mesh: TreeMesh, points: ObjectBase | ndarray, levels: list[int] | ndarray, diagonal_balance: bool = True, finalize: bool = False) → TreeMesh

Refine a tree mesh along the vertices of an object.

Parameters:

• mesh – Tree mesh to refine.

• points – Object to use for refinement.

• levels – Number of cells requested at each refinement level. Defined in reversed order from the highest octree to lowest.

• diagonal_balance – Whether to balance cells along the diagonal of the tree during construction.

• finalize – Finalize the tree mesh after refinement.

Returns:

Refined tree mesh.

Example

In the example below, the mesh is refined from the vertices of Points object. The parameters are as follows:

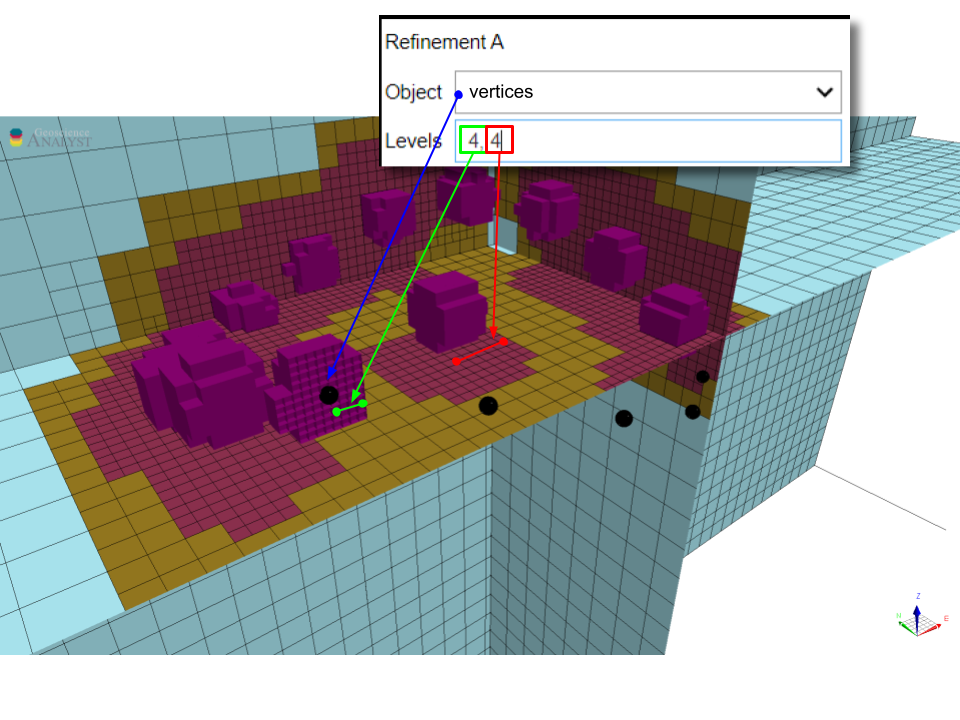
This results in a mesh that has 4 concentric shells of cells at 25 m, followed by 4 cells at 50 m around each vertex. Note that the refinement is continuous only at the 2nd octree level (50 m) where the refinements overlap.

Refine by curves

This method refines an octree mesh along the segments of a Curve object, adding cells as concentric cylinders (tubes).

static OctreeDriver.refine_tree_from_curve(mesh: TreeMesh, curve: Curve, levels: list[int] | ndarray, diagonal_balance: bool = True, finalize: bool = False) → TreeMesh

Refine a tree mesh along the segments of a curve densified by the mesh cell size.

Parameters:

• mesh – Tree mesh to refine.

• curve – Curve object to use for refinement.

• levels – Number of cells requested at each refinement level. Defined in reversed order from the highest octree to lowest.

• diagonal_balance – Whether to balance cells along the diagonal of the tree during construction.

• finalize – Finalize the tree mesh after refinement.

Example

In the example below, the mesh is refined along a closed curve. The parameters are as follows:

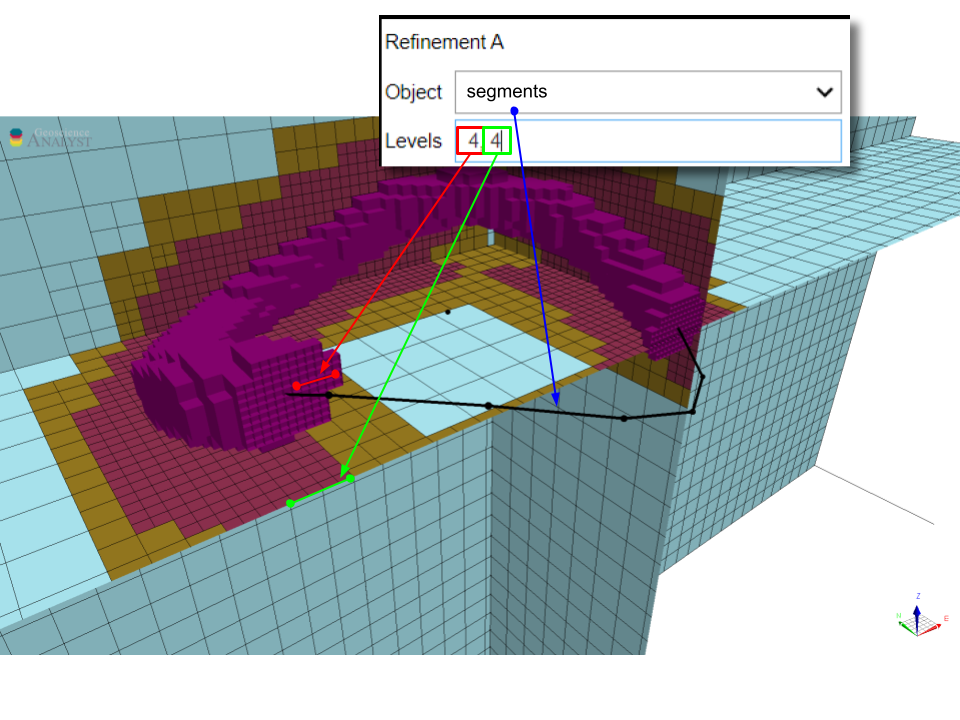
This results in a mesh with 4 concentric cylinders of cells at 25 m, followed by 4 cells at 50 m. Note that the refinement is continuous along the segments of the curve.

Refine by surface

The function is used to refine an octree mesh on a triangulated surface in 3D. It is especially useful for refining meshes along geological features, such as faults and geological contacts.

static OctreeDriver.refine_tree_from_triangulation(mesh: TreeMesh, surface, levels: list[int] | ndarray, diagonal_balance: bool = True, finalize=False) → TreeMesh

Refine a tree mesh along the simplicies of a surface.

Parameters:

• mesh – Tree mesh to refine.

• surface – Surface object to use for refinement.

• levels – Number of cells requested at each refinement level. Defined in reversed order from highest octree to lowest.

• diagonal_balance – Whether to balance cells along the diagonal of the tree during construction.

• finalize – Finalize the tree mesh after refinement.

Returns:

Refined tree mesh.

Example

In the example below, the mesh is refined around a spherical shell. The parameters are as follows:

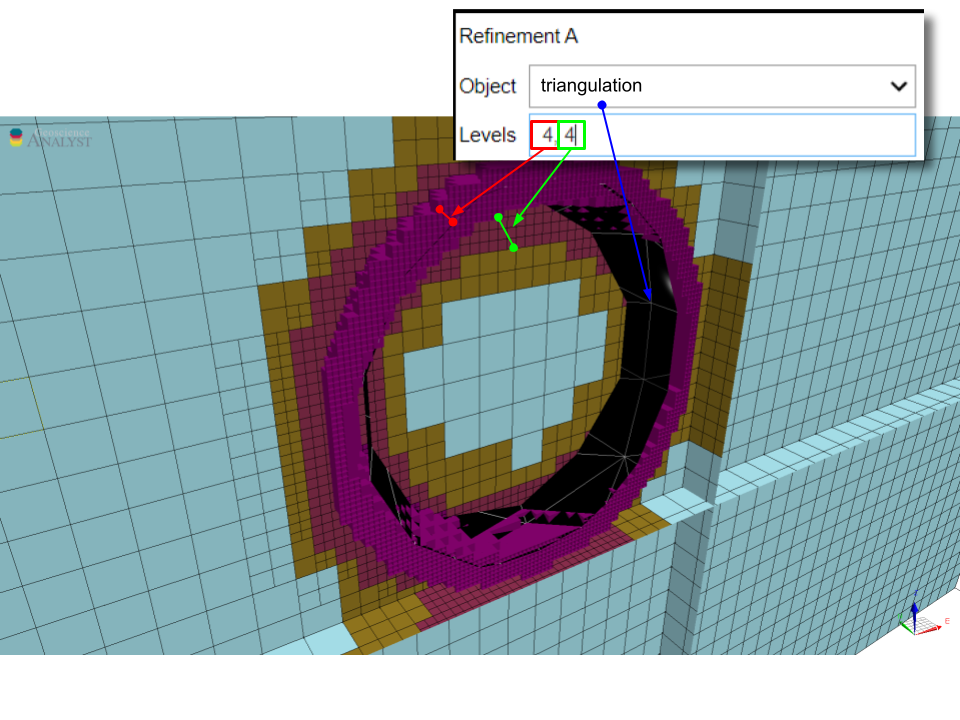
This results in shell of 4 cells at 25 m, surrounded by a shell of 4 cells at 50 m. Note that the refinement is continuous along the faces of the triangulated surface.

Refine as horizon

This method refines an octree mesh along a surface layer, or horizon. It is a faster implementation then the Refine by surface method, but it assumes the surface to be mostly horizontal (z-normal only). The surface creation relies on the scipy.spatial.Delaunay triangulation. This strategy is useful for refining the mesh on data collected along topography, such as gravity surveys. The additional parameter max_distance allows to limit the extent of refinement and avoid over-refinement in regions where the input points are sparse.

static OctreeDriver.refine_tree_from_surface(mesh: TreeMesh, surface: ObjectBase, levels: list[int] | ndarray, diagonal_balance: bool = True, max_distance: float = inf, finalize: bool = False) → TreeMesh

Refine a tree mesh along the simplicies of a surface.

Parameters:

• mesh – Tree mesh to refine.

• surface – Surface object to use for refinement.

• levels – Number of cells requested at each refinement level. Defined in reversed order from the highest octree to lowest.

• max_distance – Maximum distance from the surface to refine.

• diagonal_balance – Whether to balance cells along the diagonal of the tree during construction.

• finalize – Finalize the tree mesh after refinement.

Returns:

Refined tree mesh.

Example

In the example below, the mesh is refined along horizons defined by the vertices of Points object. The parameters are as follows:

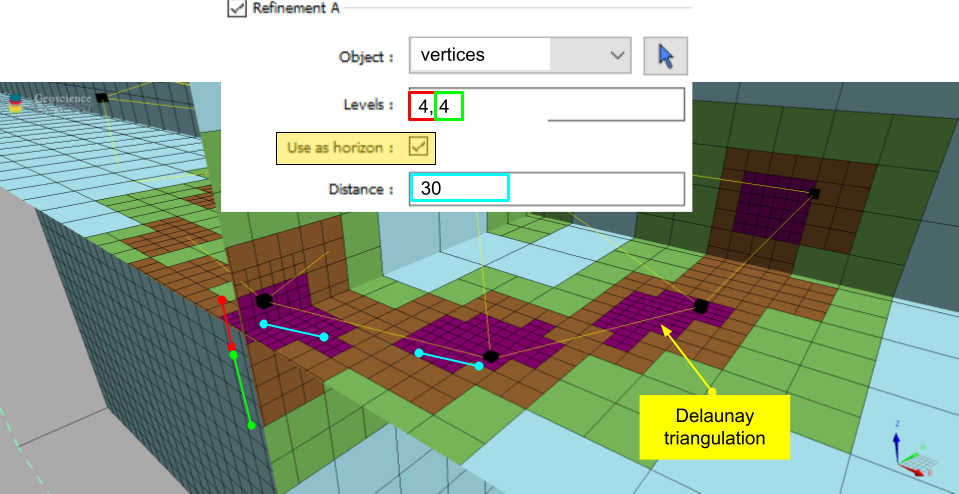
This results in a mesh that has 4 layers of cells at 25 m, followed by 4 cells at 50 m below the input vertices. Note that the refinement follows the change in elevation of the input vertices as defined by an underlying Delaunay triangulation. Beyond the max_distance of 30 m, the refinement is allowed to expand in size.